Marching Cubes
For å forstå hvorfor vi trenger en metode som dette, må vi tilbake til det jeg nevnte tidligere i modulen. I mange tilfeller kan vi ha et behov for å modellere en figur vi ikke kjenner formen til på forhånd (dvs, vi vet ikke hvilke triangler den skal bestå av). Når vi kommer oss bort fra konseptet at vi må kjenne trianglene figuren skal bestå av på forhånd, kan vi generere dynamiske figurer som kan modifiseres og modelleres med enkle matematiske formler. Det eneste kravet vi har til det vi skal modellere, er hvorvidt vi kan avgjøre om et punkt (x,y,z) befinner seg innenfor eller utenfor figuren. Ved å bruke denne informasjonen kan vi bygge opp en tilnærmet modell av det vi ønsker å modellere. Vi kan endre nøyaktigheten for å tilpasse algoritmen til applikasjonsformålet - dvs at en applikasjon som er avhengig av å kjøre i sanntid vil kunne bruke en lav oppløsning, mens en applikasjon som rendrer til et stillbilde eller lignende vil kunne bruke en høy oppløsning og generere et langt mer detaljert bilde.
Som i omtrent alle prinsipper for 3d-grafikk så kan også Marching Cubes enklest forklares ved at vi tar en titt på det samme fenomenet i 2d først. Vi ser nå på Marching Squares og ikke lenger Marching Cubes, men prinsippet er det samme. Prinsippet går ut på at vi lager en grid av punkter. For hvert av disse punktene avgjør vi hvorvidt punktet befinner seg innenfor eller utenfor objektet vi ønsker å modellere. For de firkantene som har alle punktene innenfor eller utenfor figuren, gjør vi ingenting (iallfall når vi befinner oss i 3d-rommet). For å illustrere dette kan vi se på resultatet fra en mulig implementasjon av Marching Squares.
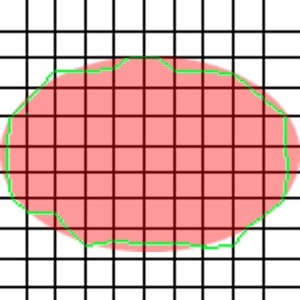
Tegningen min er noe stygg og unøyaktig, men viser forhåpentligvis hva resultatet kan bli på en grei måte. Pseudokoden antar forresten også at punktene vil lande i riktig rekkefølge automagisk, noe som ikke nødvendigvis må være tilfelle når det gjelder et polygon tegnet med så mange kanter. Vi slipper denne problemstillingen når vi beveger oss til 3d-rommet og kun tegner enkelttriangler. De verste abnormalitetene i den genererte formen i forhold til den ønskede formen, k ommer fra at vi velger punktet midt på linjestykkene som er interessante. Dersom vi interpolerer oss fram til en bedre posisjon på dette linjestykket (ut fra verdiene på de to endepunktene) vil vi få en langt bedre tilnærming. I koden til selve prosjektet gjør jeg dette.
Den røde ellipsen angir den formen vi ønsker å oppnå, den grønne streken angir resultatet fra en gjennomkjøring av Marching Squares. Punktene i gridden er der hvor de horisontale og vertikale linjene skjærer hverandre.
Pseudokode for algoritmen kan skisseres slik:
1.For hvert av punktene i gridden
1.1 sett punktets status til innenfor eller utenfor ellipsen
(ut fra formelen for en ellipse)
2.For hver av firkantene i gridden
2.1. For hvert linjestykke som har et punkt utenfor
og et innenfor figuren
2.1.1. Legg til et punkt i listen t plassert
midt mellom de to punktene
3. Tegn sekvensielle linjer mellom alle
punktene som er funnet i listen t
Da vi nå har tatt en rask titt på hvordan vi kan gjøre en slik tilnærmelse i 2d. Vi ser nå på kuber (som har 8 hjørner) i motsetning til kvadratene som vi så på med Marching Squares. Dette gjør at vi nå får en tredje dimensjon som går "innover" i skjermen. Vi ender opp med en grid som danner et rutenett i tre dimensjoner, omtrent som en legoplate full av identiske, kvadratiske blokker i f.eks. 10x10x10. Og her kommer vi inn på det som gjør algoritmen vår såpass fleksibel; dersom vi ønsker å øke nøyaktigheten til modellen vi genererer, så gjør vi enkelt og greit kubene våre mindre, men øker antallet av dem. Dette gjør at vi må prosessere langt flere punkter, men gir oss et bedre sluttresultat. I koden som er prekompilert opererer jeg med en grid som er 28x28x28, noe som gjør at vi for hver eneste frame må prosessere 21952 punkter. Dersom vi øker nøyaktigheten på gridden til 40x40x40 (noe som egentlig virker som en forholdsvis liten økning), må vi prosessere 64000 punkter. Etter litt prøving og feiling kom jeg til at 28x28x28 ga en tilfredsstillende oppløsning og fortsatt kjørte ganske rart på det som kan anses som en "grei" pc for 3d-applikasjoner i dag. La oss heller se litt mer på fremgangsmåten for å få Marching Squares over i tre dimensjoner.
|
|
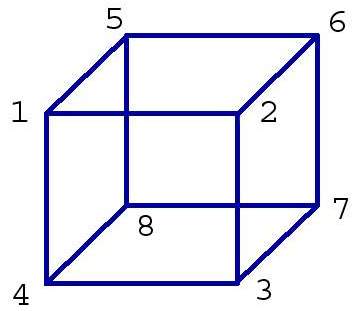
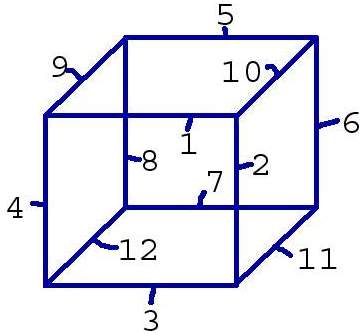
Bildene viser en enkelt kube i gridden. En grid består som sagt av et variabelt antall slike kuber, i vårt tilfelle er det magiske tallet 21952. Ettersom en kube har 8 punkter og hvert av disse punktene kan ha to forskjellige typer status (innenfor eller utenfor) får vi 2^8 = 256 forskjellige kombinasjoner av punkter som er innenfor eller utenfor modellen for en gitt kube. Dersom alle befinner seg innenfor så vil kuben være helt oppslukt av rammene rundt modellen, slik at vi ikke er interessert i å tegne noe som helst. Dersom alle befinner seg utenfor er vi i samme situasjon, bare motsatt - kuben bidrar ikke til modellen uansett. For hver av disse kombinasjonene har vi et sett med triangler som kan bli generert. Som vi skisserte i Marching Squares så fant vi et punkt som lå midt på linjen mellom punktet som var utenfor og punktet som var innenfor; i 3d vil et manglende punkt føre til at 3 linjer får en skjæring. Dette gir oss nødvendigvis tre punkter - akkurat nok til å bygge et triangel. Av de 256 ulike kombinasjonene vil som sagt 2 ikke gi noen som helst tegning, 8 av de vil gi et triangel plassert i hvert sitt hjørne av kuben .. og så videre. For en mer utbroderende forklaring anbefaler jeg at man tar en titt på linkene som er nevnt som kildemateriale.
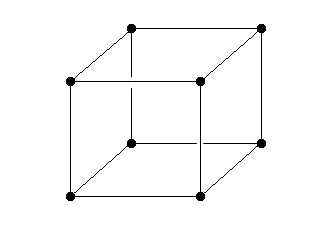
En rask bildesekvens som burde illustrere hvordan trianglene blir generert ut fra hver kube:
|
Den helt vanlige kuben vår. |
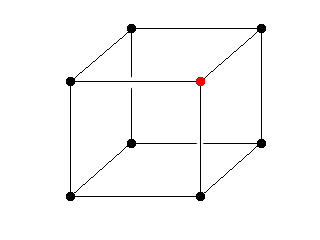
|
Vi har et punkt som befinner seg utenfor modellen vi ønsker å tegne, de resterende syv er innenfor. |
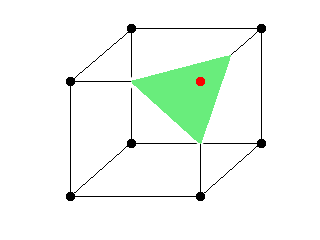
|
Vi har generert en trekant som dannes mellom midtpunktene på alle de tre linjene som nå har et punkt som er innenfor og et punkt som er utenfor modellen. |
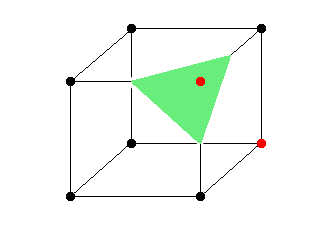
|
Vi har et punkt til i samme kube som befinner seg utenfor modellen (i koden er dette avgjort allerede før vi tegner trianglene, men det er greiere å illustrere det bit for bit). |
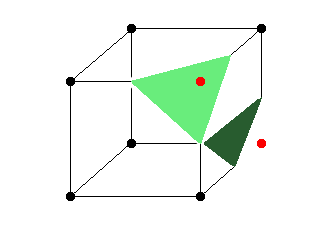
|
Vi genererer nok et triangel, denne gang på den andre siden av kuben. Som vi ser, så har nå denne enkelte kuben bidratt med to triangler til den "ferdige" modellen. Når vi kjører igjennom alle ~21.000 kubene, vil vi få en modell som ligger ganske tett opp til det vi ønsker oss. |
Her kan man tydlig se gridden og noen av trianglene som blir generert under kjøring av programmet:

|
|
Og nå, over til den delen som faktisk "makes things happen", nemlig koden:
Teknisk sett så er 'problemstillingen' med de 256 ulike kombinasjonene av manglende punkter løst på følgende måte: Vi har en lookup-tabell som inneholder 256 entries. Denne tabellen inneholder en oversikt over hvilke av de 12 linjestykkene vi skal interpolere dersom akkurat denne kombinasjonen inntreffer. Dette er angitt som et bitmønster der 1 er interpolere, 0 er uvesentlig. Et eksempel på starten av denne tabellen er gitt under:
const int mcubes::edgeTable[256] = {
0x0 , 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c,
....
}
Vi ser her at dersom vi skal slå opp på 0 i lookuptabellen (ingen er innenfor), så vil vi få '0' tilbake. Det samme gjelder for 255 (som da tilsvarer 1111 1111). Etter at vi finner ut hvilke av de 12 linjestykkene som skal interpoleres, regner vi ut punkter på disse linjestykkene som vi så lagrer i en intern 12-elementers array. Hvert linjestykke har et fast punkt i denne arrayen. For å finne ut _hvilke_ av disse punktene vi er interessert i (av disse 12), har vi en annen tabell som angir hvilke punkter vi skal lage triangler imellom for å få tegnet det ønskede trianglet. Et utsnitt av denne tabellen følger under:
const int mcubes::triTable[256][16] = {
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
...
};
Entry #0 sier at vi ikke skal ha noen triangler dersom vi har 0 i lookupverdi. Entry #1 tilsier at dersom vi har '1' i lookupverdi (dvs, hjørne nummer 1 mangler), så skal vi tegne et triangel mellom punkt 0, 8 og 3 i det statiske 12-elementer store arrayet vårt. Vi har da som en følge av behandlingen vi gjør når vi kontrollerer edgeTable oppdatert disse tre punktene til å være interpolerte punkter mellom endepunktene på det enkelte linjestykket. I praksis (som vi skal se senere) looper vi over hvert entry i tabellen (opptil 16) til vi treffer -1. Tre og tre av disse punktene danner så et triangel.
Denne kodesnutten er forholdsvis selvforklarende. Dette er hvordan det avgjøres om et punkt skal være med eller ikke være med i det endelige resultat. Vi har definert en grenseverdi (metaballs_iso_value) som sier hvorvidt punktet er innenfor eller utenfor. Alle punkter hvor utregningene ikke har ført til at vi har oversteget denne isoverdien, antas å befinne seg utenfor selve modellen. De punktene som har en verdi over isoverdien, befinner seg innenfor.
if (this->vertices[idx].flux > this->metaballs_iso_value)
{
this->vertices[idx].inside = true;
}
else
{
this->vertices[idx].inside = false;
}
Følgende kode beskriver litt om hvordan indeksen i lookup-tabellen regnes ut. Denne tar utgangspunkt i en kube i gridden vår og sjekker deretter hvert av de åtte hjørnene for hvorvidt det befinner seg innenfor eller utenfor modellen. Dersom alle åtte befinner seg innenfor vil vi få 255 i oppslagsverdi - mens dersom alle befinner seg utenfor vil vi få 0. I disse to tilfellene har vi 0x0 som entry i edgeTable, noe som sier at vi ikke ønsker å interpolere noen av kantene våre. Alle andre kombinasjoner vil generere et sett med interpoleringer av kanter og (litt lenger ned) et eller flere triangler. Dette er et lite utsnitt av selve rutinen (som vil ha 8 if-setninger, ikke bare to).
if (this->vertices[idx].inside) lookup |= 128; if (this->vertices[idx+1].inside) lookup |= 64;
Koden under er et utsnitt av hvordan interpoleringen av de ulike linjestykkene foregår. Verdien vi fikk fra tabellen vi fant ut oppslagsindexen til i koden overfor, ANDes med verdier som tilsvarer 2^0 -> 2^11. Dette gir oss hvert av de tolv linjestykkene som befinner seg i en kube. Deretter plasserer vi et punkt inn i dette 12-punkters arrayet som er omtalt tidligere, ferdig interpolert fra interpoleringsrutinene våre.
if (this->edgeTable[lookup] & 1)
this->verts[0] = this->mb->interpolate(
this->vertices[idx + this->size_y +
(this->size_y * this->size_z)],
this->vertices[idx + 1 + this->size_y +
(this->size_y * this->size_z)]
}
Koden som skal presenteres her gjør selve uttegningen. Vi lager en for-løkke som går igjennom entryene som er gjort for en spesifikk lookup-del av triTable. Som jeg viste lenger opp, er dette verdier av f.eks. 0,8,3. Dette tilsier at vi ønsker å se på punktene vi har interpolert i 12-elementers arrayet vårt på element 0, 8 og 3. Disse danner så et triangel. Grunnen til at jeg i denne kodeseksjonen har valgt å ha to looper, en som looper fra triangel til triangel og et som looper over de ulike punktene i trianglet, er fordi man skal ha mulighet til å rendre hele figuren i wireframe dersom man ønsker det. Akkurat det punktet forutsetter at vi er i stand til å tegne enkeltstående linelooper på tre punkter hver, noe som gjør at vi ikke kan bruke en fast loop som bare tar tre og tre punkter (som man gjør med vanlig GL_TRIANGLES som brukt her). Legg merke til at vi looper over verdiene i triTable fram til et element er -1 som betyr at vi ikke har flere triangler som skal tegnes. Vi angir også normalene for hvert enkelt av de interpolerte punktene, slik at lyssettingen vår skal fungere som ønsket.
for (i = 0; this->triTable[lookup][i] != -1; i+=3)
{
glBegin(GL_TRIANGLES);
{
for (j = i; j < (i+3); j++)
{
glNormal3f(
(float) this->verts[this->triTable[lookup][j]].normal_x,
(float) this->verts[this->triTable[lookup][j]].normal_y,
(float) this->verts[this->triTable[lookup][j]].normal_z
);
glVertex3f(
(float) this->verts[this->triTable[lookup][j]].x_pos,
(float) this->verts[this->triTable[lookup][j]].y_pos,
(float) this->verts[this->triTable[lookup][j]].z_pos
);
}
}
glEnd();
}
Ettersom vi nå har sett på den delen av koden som gjør selve uttegningen og logikken bak "parsingen" av de ulike kubekombinasjonene, skal jeg også ta en rask tur innom de to rutinene som gjør at ting fungerer som de skal i praksis. Den første rutinen er en enkel interpoleringsrutine, definert som 'inline' i c++ ettersom den vil bli kjørt en gang for hvert punkt i gridden (som nevnt er dette ca. 21.000 punkter i den prekompilerte versjonen). I praksis gjør dette at kompilereren setter inn koden direkte, i stedet for at vi får et funkjonskall med alle de tregheter det medfører (som stack (tror ikke den blir med i inline-statements) og parameterparsing).
Selve utregningen av de interpolerte punktene burde det ikke være nødvendig å forklare videre, vi regner ut en vekt i forhold til de to punktene og hvordan det avgjørende punktet skal interpoleres i henhold til dem. Dette gjøres i henhold til parameteret 'flux' som angir hvor mye et punkt blir påvirket av de ulike metapunktene / kraftpunktene våre. Selve utregningen av denne verdien gjøres i rutinen som er beskrevet et segment lenger ned.
inline vertex interpolate(vertex v1, vertex v2)
{
vertex v;
double diff;
diff = (this->iso_value - v1.flux) / (v2.flux - v1.flux);
/* finner hvor på linjestykket punktet ligger */
v.x_pos = v1.x_pos + (v2.x_pos - v1.x_pos) * diff;
v.y_pos = v1.y_pos + (v2.y_pos - v1.y_pos) * diff;
v.z_pos = v1.z_pos + (v2.z_pos - v1.z_pos) * diff;
v.flux = (v1.flux + v2.flux) * 0.5;
/* regner ut en gjennomsnittsnormal ut
fra normalene på de enkelte punktene */
v.normal_x = v1.normal_x + (v2.normal_x - v1.normal_x) * diff;
v.normal_y = v1.normal_y + (v2.normal_y - v1.normal_y) * diff;
v.normal_z = v1.normal_z + (v2.normal_z - v1.normal_z) * diff;
return v;
}
Dette er koden som regner ut hvordan metapunktene / kraftpunktene påvirker hvert enkelt element vi ønsker å se på i gridden. Først initialiserer vi flux-verdien for dette punktet til 0, før vi kjører en rask løkke over hvert av metapunktene for å se hvor mye det aktuelle punktet blir påvirket. I praksis gjør jeg dette ved å regne ut en helt vanlig vektorlengde mellom gridpunktet og metapunktet. Formelen jeg valgte å benytte meg av er (kraft^2 / (x_lengde^2 + y_lengde^2 + z_lengde^2), noe som gir oss en funksjon som avtar med etterhvert som avstanden øker. Grunnen til at den første kraft-verdien er dyttet inn i en fabs, er for at vi skal kunne ha negative effekt fra et metapunkt. Jeg har ingen kode som illustrerer dette i praksis, men det burde ikke være verre enn bare helt enkle, små modifikasjoner for at man skulle kunne ha et gitt punkt som påvirker hele gridden i negativ retning. Det er flere gode, pene eksempler på hvordan dette kan gjøres (se thermo plastique av inf, tilgjenglig fra http://www.pouet.net/prod.php?which=5558). Dette er en av mange mulige utvidelser som kan foreslås som et prosjekt under en senere avvikling av kurset.
inline double get_vertex_value(vertex v)
{
double flux = 0.0;
for (i = 0; i < num_metapoints; i++)
{
/* regner ut hvor langt det er til dette
punktet fra det gitte metapunktet */
length_x = metapoints[i].x_pos - v.x_pos;
length_y = metapoints[i].y_pos - v.y_pos;
length_z = metapoints[i].z_pos - v.z_pos;
/* regner ut styrken som dette punktet påvirkes med */
flux += fabs(metapoints[i].power) * metapoints[i].power / (
length_x * length_x +
length_y * length_y +
length_z * length_z + 1);
}
return flux;
}
Det er også plassert en del kommentarer i koden (men den er ikke "overkommentert", så en viss forståelse av C/C++ kreves.

