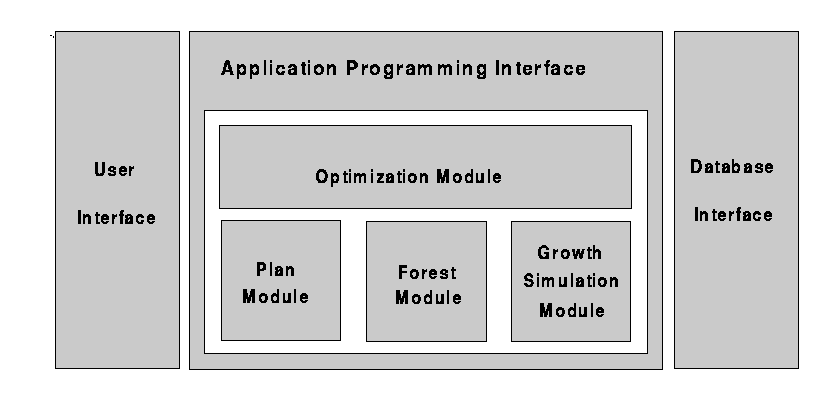
FIGURE 1. The EcoFrame architecture.
Oddvar Kloster
Research Scientist
Department of Optimisation
SINTEF Applied Mathematics
P.O.Box 124, Blindern
N-0314 Oslo, Norway
Phone: (+47) 22 06 73 00
Fax: (+47) 22 06 73 50
Email: okl@math.sintef.no
Gunnar Misund
Senior Research Scientist
Department of Spatial Modelling
SINTEF Applied Mathematics
P.O.Box 124, Blindern
N-0314 Oslo, Norway
Phone: (+47) 22 06 73 00
Fax: (+47) 22 06 73 50
Email: gmi@math.sintef.no
In order to supply the Norwegian forest associations with IT tools to support their planning processes, a research and development project was initiated in 1994. Results from earlier feasibility studies have been reported in (Misund et al. 1996a, 1996b; Adhikary et al. 1997). This paper reports some of the results from the project, which has been co-ordinated by SINTEF Applied Mathematics, involving personnel from the forestry sector as well from the computer science community (SINTEF 1997).
The paper is organised as follows. In section 2 we discuss the underlying forest model which the EcoFrame framework is based upon. We proceed in section 3 by presenting the framework structure and its main components. A pilot application, Ecoplan, is described in section 4. We also demonstrate the configurablity of the framework by tuning Ecoplan to handle two widely differing cases, one from Norwegian forestry and the other based on Indonesian conditions. The results from these two cases are discussed in section 5 and 6. The paper is closed by some final remarks and suggestions for further work.
The EcoFrame framework is designed upon a compartment based forest management model. Variants of such models are applied widely in Scandinavia, Canada and USA.
The basic assumption is that the forest may be partitioned into a set of spatially well defined areas, which will be called treatment units (TU). In addition, we introduce the notion of a region, which is an arbitrary subset of TUs. Different regions may be disjunct, overlap or contain each other. Each TU is considered homogeneous with respect to a set of properties, such as average height, site index and species distribution, which may vary over time or be time independent. The set of these state variables expresses the condition of the TU at a given point in time. We assume that the information embedded in the state vector is sufficient for the planning process. In the Norwegian case described in Section 5, the TU corresponds to the stand notion (Fig. 2), but in the Indonesian case (Section 6), we define the TU to be a single tree in the rain forest (Fig. 10).
The scheduling problem to be solved by a EcoFrame based application is to assign treatment programmes (TP) for each TU over a given planning horizon which is divided into a number of planning periods. A treatment programme has a certain duration (fixed or adjustable), given in a number of planning periods, and affects the state of a TU. Typically, the TP is defined by a set of criteria for when the programme is applicable. In addition, the result of the treatment may also be specified. Both the criteria and the result are specified in terms of the state variables. A special case of the TP is the "do-nothing" or "let-grow" programme.
We also assume there exists a growth model enabling forecasting the future state of the TUs, i.e. to compute new values for the state variables.
In order to produce "good" plans, criteria defining the "goodness" must be provided, optionally accompanied with a set of constraints. Both criteria and constraints must be defined in terms of the state variables. We may restrict criteria and constraints to apply only to a specified region.

FIGURE 1. The EcoFrame architecture.
The framework is illustrated in Figure 1 . The main components are a forest module, a growth simulation module, a plan module and an optimisation module. The interfaces between the modules are well defined, allowing substitution of different versions of the modules when composing a specific application. Further flexibility is obtained by configurability within each module.
Similar modular frameworks exist, e.g. as used in ArcForest (ESRI 1997). That framework does however not include optimisation.
The forest module is responsible for managing all the data describing the forest. This includes the division of the time horizon into planning periods, the number and geometry of treatment units, their topology, i.e. neighbour relation, regions and initial states. The state vector definition may contain any number of variables of integer, real or character type. The forest module also contains the definition of the possible treatment programmes. The simplest TPs are basic TPs, e.g. "Let Grow" or "Clearcut". These may be sequenced into aggregated TPs describing common treatment cycles. TPs may contain conditions on the state for their applicability and have fixed or adjustable duration.
The growth simulation module contains the growth model of the forest. Its basic functionality is to be able to simulate a stand state over a period in which a given basic TP is applied. One will typically create different stand simulator modules which simulate different types of forest and which have different requirements on variables present in the state definition and on TP types handled.
The plan module is responsible for managing treatment plans, which consist of a local plan for each treatment unit. A local plan is a sequence of TPs covering the entire time horizon. The module uses the growth simulation module to calculate the state evolution in a given plan and has functionality for altering a plan.
The optimisation module may be configured with the criteria to be optimised and their relative importance. The module then uses the services of the other modules to search for the best plan according to the criteria definition. After optimisation, the best plan found is available from the plan module.
These four modules are embedded in the Application Programming Interface (API), which provides a well-defined set of functions which may be requested from the modules. The API has a client-server connection to a User Interface to allow running the system in a distributed environment, and to use different user interfaces. The API also connects to the sources for the various data that are required by the system.
For more details on the framework, see (Krogstie 1996; Arthur 1998; Hasle et al. 1998).
The forest module which is implemented offers management of an unlimited set of treatment units, which may be arranged arbitrarily in any desired number of regions. The state vector is configured runtime, i.e. the number and their types (real, integer, character) are decided by the user, who also may specify legal intervals and/or values for each state variable. The forest module also manages a range of additional information, such as terrain data and TU topology.
Two different growth simulation modules are implemented. One is based on growth tables for the main Norwegian species, while the other one targets tropical rain forest and is based on the simple assumption that the annual average diameter increment of any commercial specie is around 1 cm per year.
The available types of optimisation criteria are:
There is one general optimisation module which works as follows: An initial solution is generated by assigning a local plan for each stand, without regarding the optimisation criteria. We then try to improve on this plan using a simple iterative improvement technique. At each iteration, an adjustable duration TP is selected, and a set of new plans with different durations for this TP are generated. The best of these becomes the new current plan. This technique produces good plans for widely different problems, but is less efficient than dedicated algorithms because of its generality. For more information on iterative improvement techniques, see e.g. (Reeves 1993).
The Ecoplan application is run from a simple graphical user interface, using the application programming interface provided in the framework. The database interface is quite simple, using flat ASCII files for importing data and exporting schedules and related information.
The treatment programmes are different compositions of basic treatments such as thinnings and clear-cutting. The planning horizon is fairly long, consisting of 250 periods, each with one year duration. Since the average harvesting cycle is around 80 years, this implies multiple rotations planning.
According to the Norwegian criteria of sustainable forest management (Aanderaa et al. 1996), the case area is classified into three different regions ( Figure 2 ):
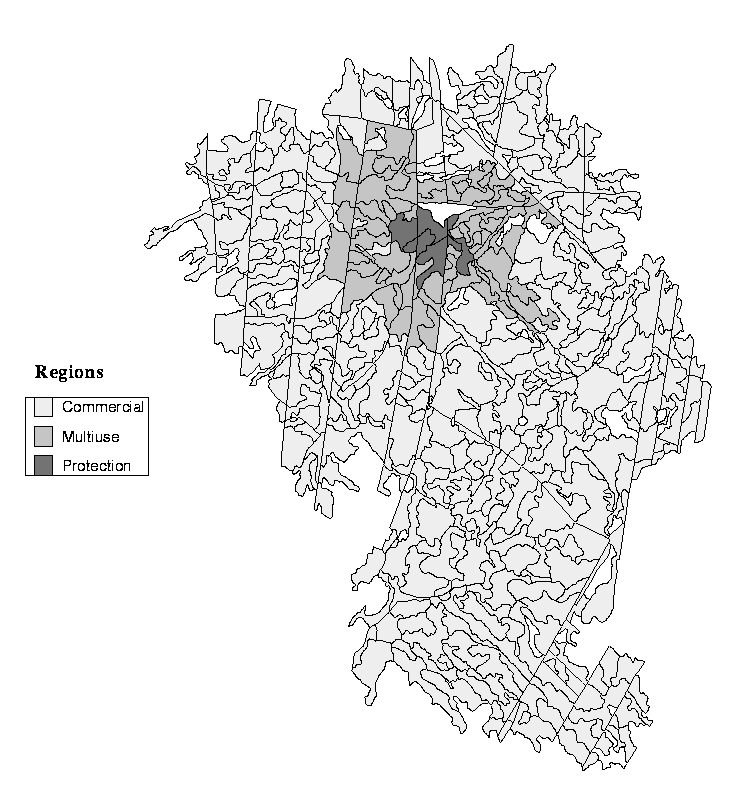
FIGURE 2. Treatment units in the Norwegian case.
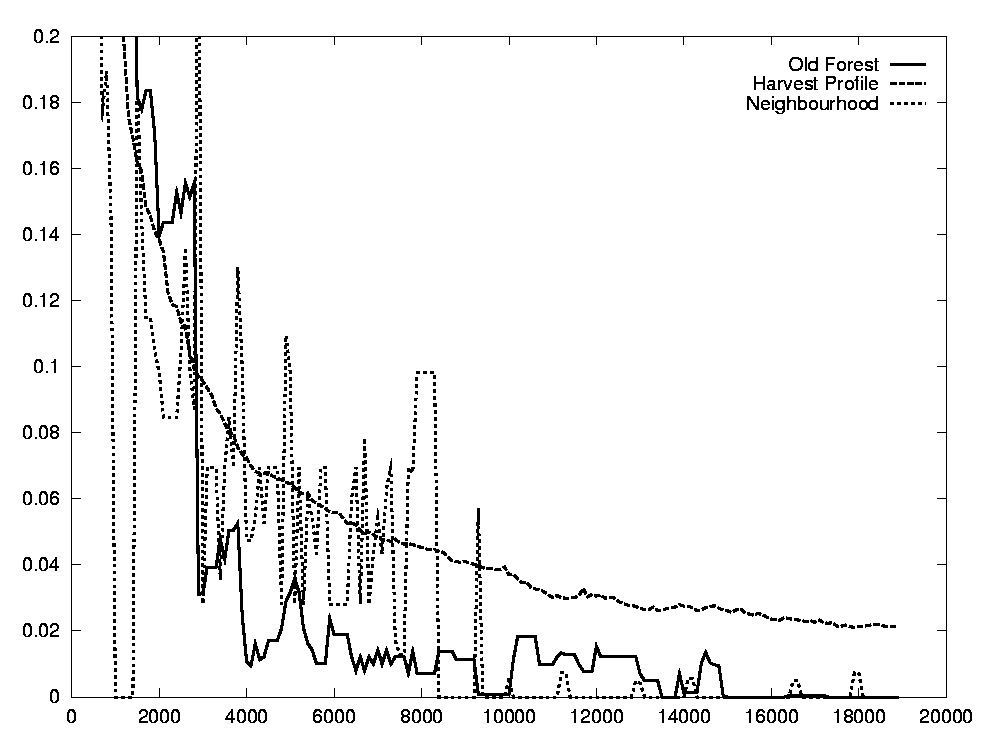
FIGURE 3. Criteria progress.
The progress of the optimisation is shown in figure 3 . The x-axis shows the number of iterations. The y-axis shows penalty values for the criteria, zero meaning that the criterion is fulfilled completely. We see that the values of the criteria fluctuate a bit, but generally move towards zero. At around 13500 iterations, both the Old Forest and Neighbourhood criteria are fulfilled at the same time, and generally remain so after. We stop optimising after 19000 iterations.
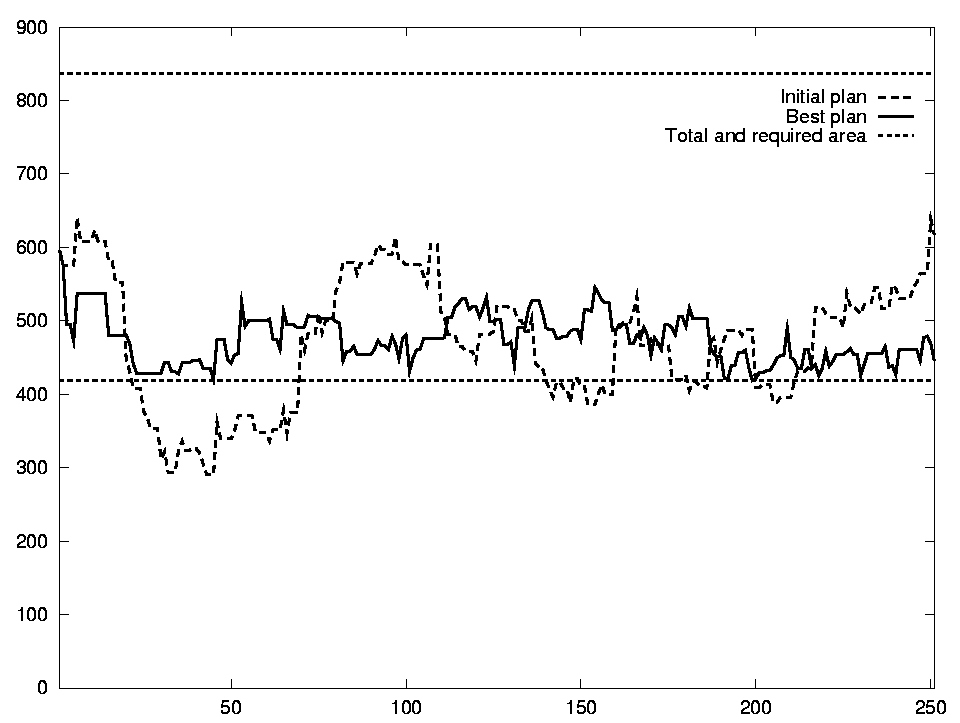
FIGURE 4. The Old Forest criterion.
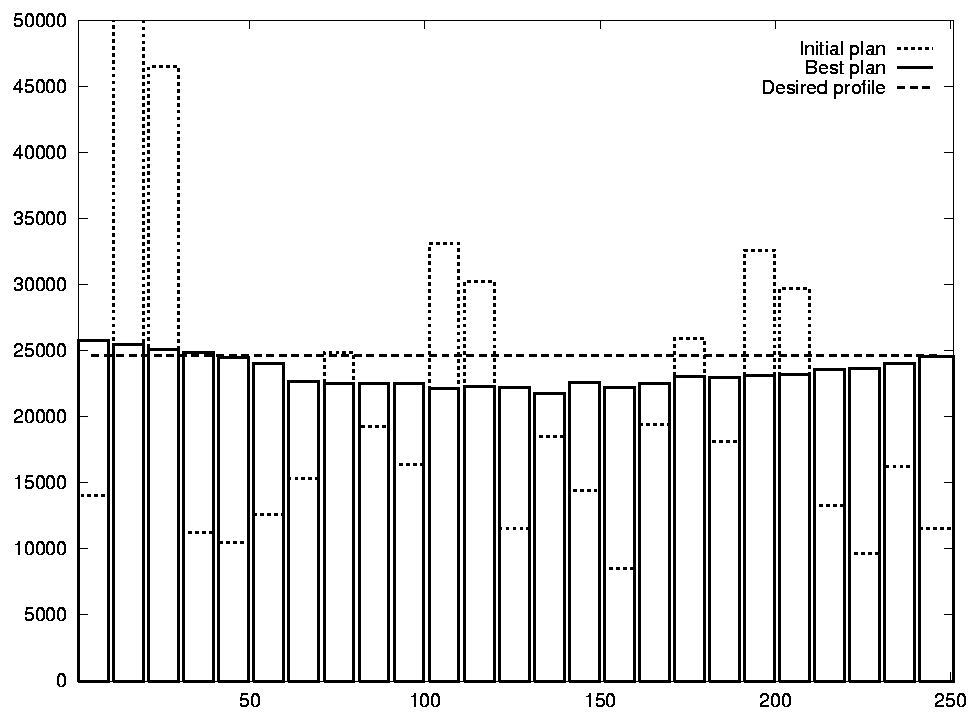
FIGURE 5. Harvest Profile criterion.
The improvement for the Old Forest and Harvest Profile criteria are visualised in Figures 4 and 5 respectively. For Old Forest, the x-axis is time, and the y-axis represents the area covered by old forest. We see that in the initial plan, there is too little old forest between periods 20 and 70. In the final plan, the fraction of old forest is above the required 50% at all times. For Harvest Profile, the vertical bars measure the volume of timber harvested in each 10-year period. Here we see that the final solution is a much better approximation of the desired profile than the initial solution. All in all, the plan fulfills the specified criteria very well.
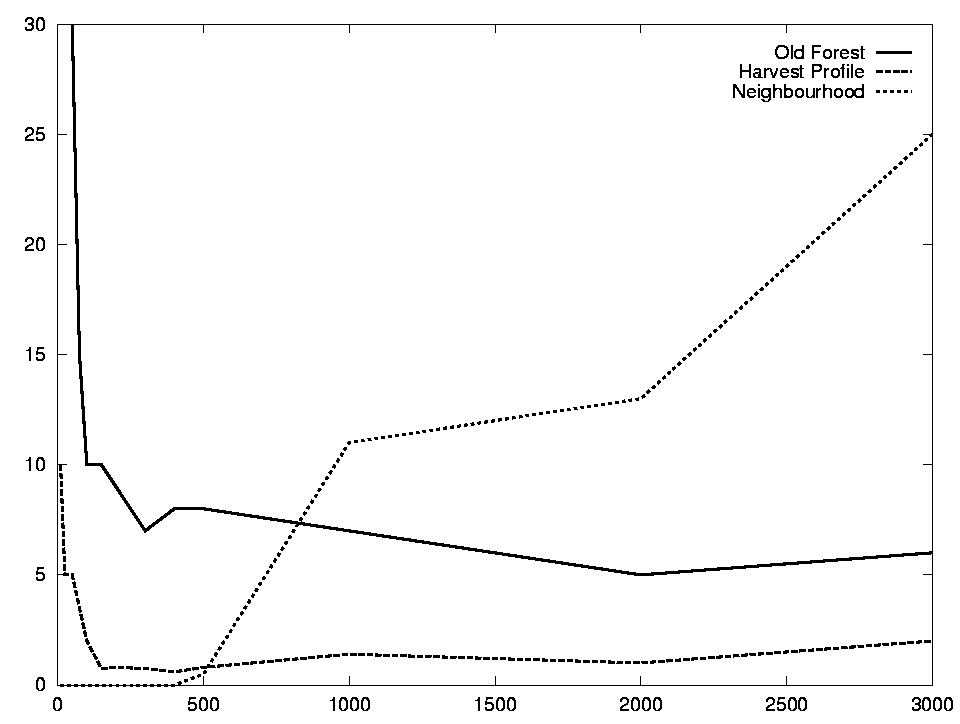
FIGURE 6. Final values for different region sizes.

FIGURE 7. Number of iterations for different region sizes.
In the second series, we keep the region size constant to 200, but vary the length of the time horizon between 10 and 1000 years. Figure 8 shows the final criteria values. The X-meter criterion is fulfilled for all horizons. The two other criteria get worse with longer horizons, but their values divided by the horizon length are fairly constant, meaning that so are the average deviation from the desired volume profile and desired old forest percentage. Figure 9 shows the number of iterations required to reach these values. These curves show a roughly linear dependency on the number of time periods.
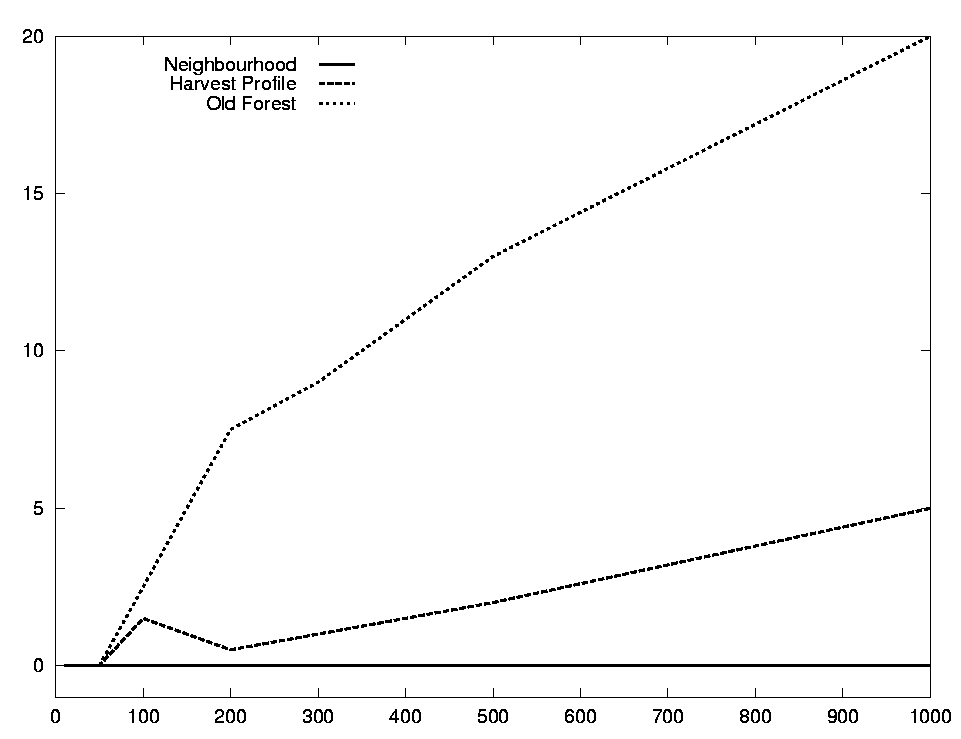
FIGURE 8. Final values for different horizon lengths.
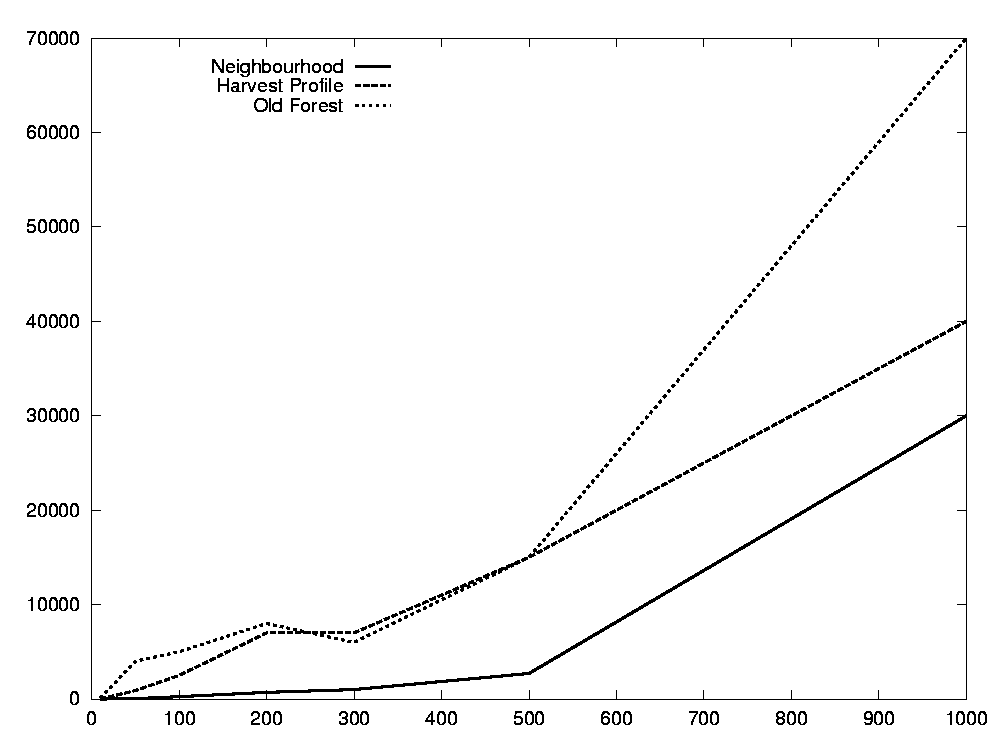
FIGURE 9. Number of iterations for different horizon lengths.
In our case example, we deviate from the one year scope of the operational plans, and stretch the horizon to 35 periods of one year each. For obvious reasons, this model restricts the planning to handle only single rotation scheduling. Hence, the only allowable plan is composed of the basic treatments "Let Grow" and "Cut".
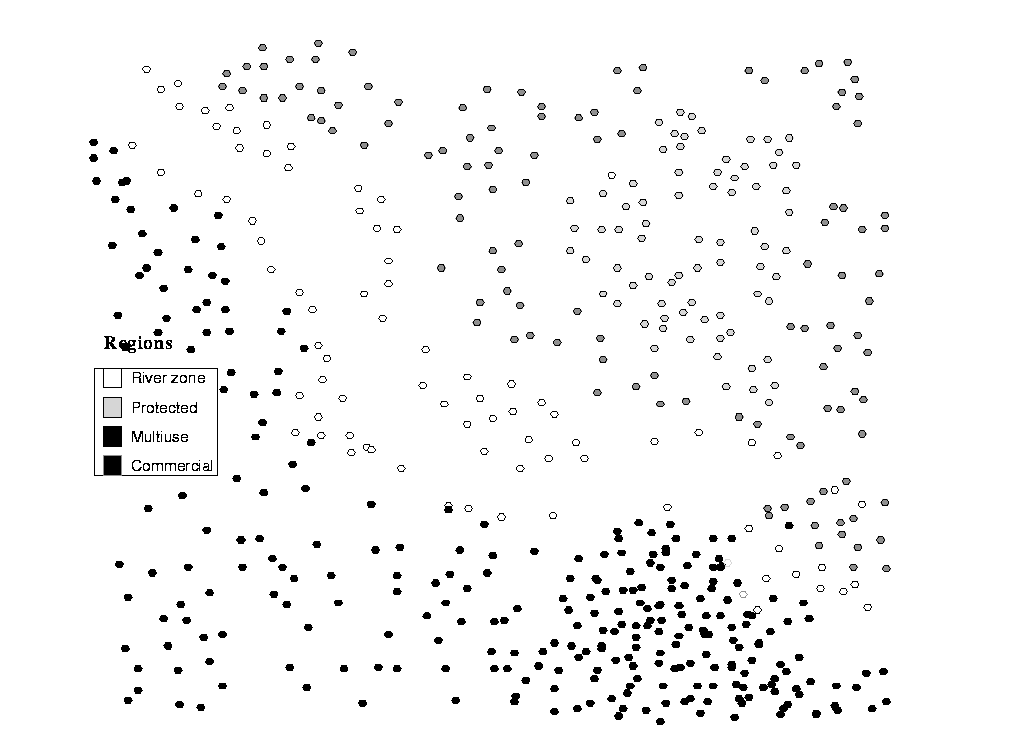
FIGURE 10. Indonesian tree map.
The data in this case is generated randomly. The area contains 560 trees in four regions as shown in Figure 10 . In the River Zone, the trees may not be touched at all, so this region is locked. In the Protected region, trees should be cut spatially evenly, and there should always be a certain number of old trees producing seeds. For this, we use an Old Forest criterion, and a Cluster criterion. For this case, neighbours are defined as the trees within a certain radius. There is a Cluster criterion on the Multiuse region also. For the entire area, we define an Value Profile (based on the price and volume information in the state vector), which should be equal in each two-year period.
Optimising this case, we reach a stable solution in around 5000 iterations. The Cluster criterion for the Multiuse region is slightly unfulfilled, the harvested value profile is as shown in Figure 11 , and the other criteria are fulfilled.
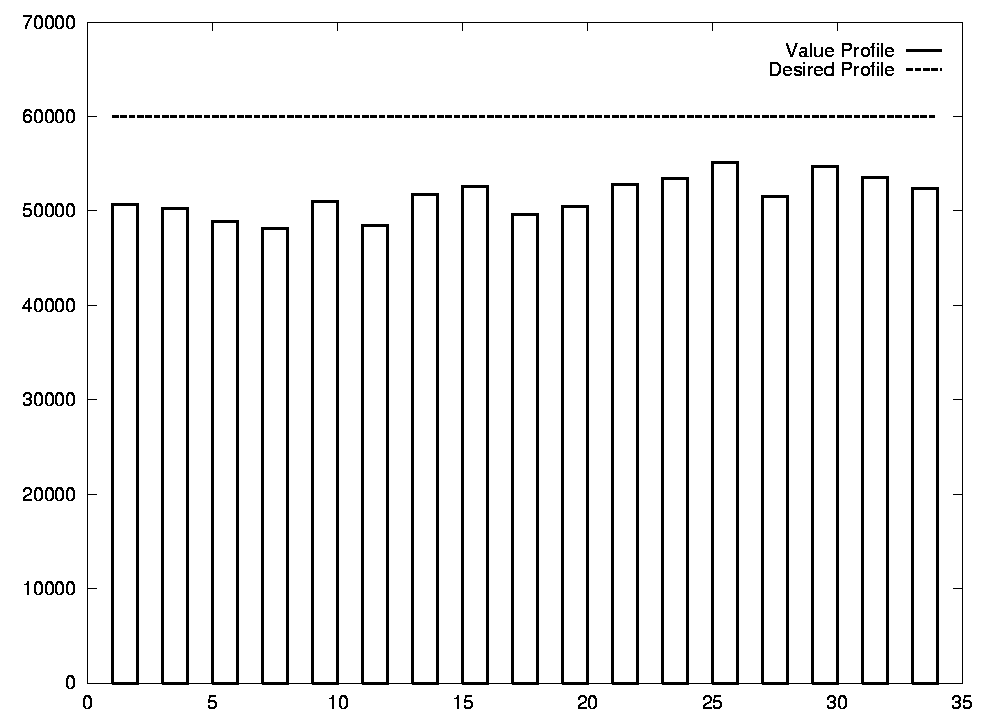
FIGURE 11. Final Value Profile.
In addition, we have conducted a set of performance investigations which indicate that the Ecoplan application is capable of handling large problems within reasonable time limits, regarding both the number of treatment units involved, and the size of the planning horizon.
The SINTEF Ecoplan Project is still in progress, and in the following we outline some of the scheduled work focusing on improvements and enhancements of EcoFrame.
Adhikary, J., G. Hasle, and G. Misund. 1997. "Constraint Technology Applied to Forest Treatment Scheduling." Proceedings of the Third International Conference on the Practical Application of Constraint Technology (PACT97). London: Practical Application Company Ltd. ISBN 0 9525554 4 1.
Arthur, J. K. 1997. "Ecoplan User Guide." To appear as a SINTEF report.
Arthur, J. K. 1998. "Ecoplan System Documentation." To appear as a SINTEF report.
ESRI. 1997. "ArcForest Homepage." Web page: http://www.esri.ca:80/af/
Hasle, G., O. Kloster, and A. Lokketangen. 1998. "Interactive Planning for Sustainable Forest Harvesting." Submitted to The Annals of OR - Special Issue on Operations Research Models in Natural Resources.
Krogstie, B. 1996. "Kravspesifikasjon for Okoplan 1." SINTEF Report STF42 F96104 (in Norwegian).
Ministry of Forestry of The Republic of Indonesia. 1997. "Timber Production." Web page: http://mofrinet.cbn.net.id/h_page/timber.htm
Misund, G., B. S. Johansen, and G. Hasle. 1996a. "Integration of Geographical Information Technology and Constraint Reasoning - A Promising Approach to Forest Management." SCANGIS '95 - Proceedings of the 5th Research Conference in GIS. Trondheim, Norway. ISBN 82-993522-07.
Misund, G., B. S. Johansen, and G. Hasle. 1996b. "Solving the Clear-Cut Scheduling problem with Geographical Information Technology and Constraint Reasoning." Proceedings of the Third International Conference/Workshop on Integrating GIS and Environmental Modelling. Santa Fe, New Mexico, USA.
Reeves, Colin R. (ed.) 1993. Modern Heuristic Techniques for Combinatorial Problems. Blackwell Scientific Publications.
SINTEF. 1997. "List of Projects." Web page: http://www.oslo.sintef.no/am/Opti/optim.listofproj.html
Gunnar Misund graduated as Master of Science in mathematical modelling from the University of Oslo in 1993. His is affiliated with SINTEF Applied Mathematics as a senior research scientist in the Department of Spatial Modelling. His main research interests are Geographic Information Technologies and their applications to Natural Resources Management. He is currently working on a PhD thesis on dynamical terrain modelling.