Algoritmeanalyse
- Hva er algoritmeanalyse?
- Store O-notasjon
- Hvordan bestemme en algoritmes arbeidsmengde/kompleksitet?
- Hvordan forutsi hvor lang tid det vil ta å kjøre et program?
- Logaritmer
- Arbeidsmengden til noen sorterings- og søkealgoritmer
Innledning
I algoritmeanalysen er man interessert i å undersøke og si noe om hvor effektiv en gitt algoritme er. Det er to hovedaspekter ved algoritmers effektivitet:
-
Tidsforbruk
Hvor lang tid tar en algoritme på å løse et problem i forhold til en annen algoritme? Hvordan øker tidsbruken når problemet vokser seg stort? -
Plassforbruk
Hvor mye internminne (evt. også eksternminne, dvs. disk etc.) bruker algoritmen i prosessen med å løse et problem av en viss størrelse? Hvordan øker plassbruken med problemstørrelsen?
I begge tilfellene er vi opptatt av hvordan tid- og plassforbruket øker når vi øker størrelsen på problemet algoritmene skal løse. Problemets størrelse, eller størrelsen på input, uttrykkes ofte ved parameteren N, som er et positivt heltall. Hvis det er en sorteringsalgoritme det er snakk om, vil N være antall elementer som skal sorteres.
I algoritmeanalysen er vi generelt ikke interessert i å vite nøyaktig hvor mye tid en algoritme bruker, men prøver heller å angi hvilken størrelsesorden løsningen ligger i. "Store O"-notasjon (Big-Oh) er en grov måte å angi tidsforbruk på.
Det er i praksis to måter å tilnærme seg algoritmeanalysen. Enten er vi interessert i hvordan algoritmen oppfører seg i en "normal", eller "gjennomsnittlig" situasjon, eller så er vi interessert i hvor effektiv algoritmen er for de "verste tilfeller" av input. I det siste tilfellet ønsker vi en slags garanti for at en metode ikke overstiger en viss øvre grense når det gjelder bruk av tid eller minne. Det er denne typen analyse ("worst case") som er den vanligste, og den som er den enkleste å utføre. Det viser seg imidlertid at i mange anvendelser er det viktigs å kunne si noe om gjennomsnittlig oppførsel. Dessverre er denne type analyser ofte meget kompliserte.
Kjøretid
- Ønsker å måle hvor effektiv en algoritme er.
- Kjøretid avhenger av
- Antall operasjoner som utføres i algoritmen.
- Ytre faktorer som for eksempel maskinvare og programmeringsspråk.
- Antall operasjoner kan ofte uttrykkes som en funksjon av størrelsen på input-datasettet (N).
- Hvordan ser kjøretiden ut når inputstørrelsen øker.
Eksempel 1 - Nedlasting av filer over internett
Gitt at det tar 2 sekunder å sette opp en internettforbindelse, og at man deretter kan laste ned 1.6K/sekund.
Hvis filen som skal lastes ned er på N kilobytes, vil tiden det tar å laste den ned kunne uttrykkes som:
Kjøretid tilnærmet proporsjonal med inputstørrelsen - lineær algoritme.
Eksempel 2 - Finne det minste elementet i en tabell
Algoritme:
Input: Tabell med N heltall, tab
Output: Den minste elementet i tabellen, min
Lokale variabler: Indeksvariabel, i
Kildekode
Opptelling av operasjoner
- Teller som regel ikke opp operasjonene så detaljert som dette
- For store N dominerer operasjonene som skjer inne i løkka.
- Antall ganger den/de dominerende operasjonene utføres, definerer algoritmens orden.
- Algoritmen over er lineær (har orden N)
En algoritmes arbeidsmengde - Store O-notasjon (Big-Oh)
Matematisk definisjon
- Av definisjonen kan vi lese at Store-O gir en øvre grense for kjøretidsfunksjonen T(N).
- Er generelt ikke interessert i å vite nøyaktig hvor lang tid det vil ta å kjøre et program, men snarere å finne hvilken størrelsesorden løsningen ligger i.
- O-notasjon er en veldig grov måte for å klassifisere tidsforbruk. Vi forkorter så mye som mulig, og stryker både lavereordensledd og konstanter.
Noen vanlige funksjonsklasser
Hensikten med "Store-O" er å klassifisere arbeidsmengden til algoritmer i hovedgrupper, ettersom hvordan funksjonene vokser for store verdier av N (størrelsen på input-datasettet).
Noen funksjoner som beskriver algoritmers arbeidsmengde:
| Klasse | T(N) | Oppførsel |
|---|---|---|
| Konstant | O(1) | 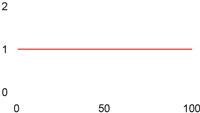
|
| Lineær | O(N) |
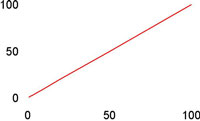
|
| Kvadratisk | O(N2) | 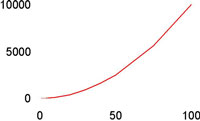
|
| Kubisk | O(N3) | 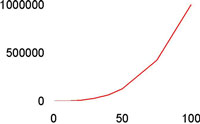
|
| Logaritmisk | O(logN) | 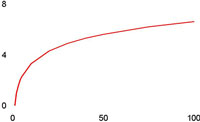
|
| Loglineær | O(NlogN) | 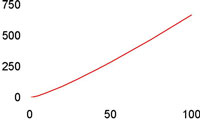
|
- For store datamengder (N stor) vil verdien til en funksjon bestemmes av det dominerende leddet til funksjonen.
- For små verdier av N vil ofte valg av algoritme være mindre viktig, siden forskjellen mellom den raskeste og den tregeste algoritmen vil være marginal.
- Det kan være slik at en kurve er bedre enn en annen for små verdier av N, men dårligere for store verdier av N.
Løkker
- Når vi beregner arbeidsmengden til en algoritme, vil operasjoner som står inne i løkker dominere over operasjoner som står utenfor, fordi de gjentas mange ganger.
- Arbeidsmengden til en løkke er gitt som arbeidsmengden til setningen(e) inne i løkka multiplisert med antall iterasjoner.
- Arbeidsmengden til setninger som står inne i nøstede løkker gitt som arbeidsmengden til setningene multiplisert med størrelsen til alle løkkene.
- Løkker som kommer etter hverandre gir lineær arbeidsmengde.
- Hvis vi skal forsøke å gjøre en algoritme mer effektiv, må vi se om det går an å forenkle en eller flere operasjoner. Da er det operasjonene som utføres mange ganger vi må se nærmere på. I praksis betyr det operasjoner som utføres i løkker.
Oppgave
- Gjør en grov opptelling av antall operasjoner i kildekoden nedenfor
- Angi arbeidsmengden med Store-O notasjon
Beregning av kjøretid
Når vi kjenner arbeidsmengden til en algoritme, og vi vet hvor lang tid det tar å løse problemet for en bestemt verdi av N, er det mulig å beregne (grovt) hvor lang tid det vil ta å løse et større problem.
Oppgave
Anta at det tar 0.5 ms å kjøre et program når N=100. Hvor lang tid vil det da ta å kjøre programmet når N=1000 hvis arbeidsmengden er
- lineær ?
- kvadratisk ?
- kubisk?
Kontroll av algoritmeanalyse
- Når vi har utført en algoritmeanalyse, er vi interessert i å finne ut hvor nøyaktig/"riktig" den er.
- En måte å gjøre dette på, er å sammenlikne beregnet kjøretid og empirisk/observert kjøretid for økende verdier av N.
- Hvis vi har funnet at arbeidsmengden til en algoritme er O(F(N)), og vi finner at reell kjøretid er T(N), kan vi se på forholdet T(N)/F(N), og se på hvordan dette endres for økende verdier av N.
- Øker: Arbeidsmengden er underestimert
- Går mot null: Arbeidsmengden er overestimert
- Går mot en konstant verdi: Godt estimat.
Eksemplet nedenfor er basert på empiriske kjøretider for en gitt algoritme, og er hentet fra "Data Structures & Problem solving using Java" av Mark Allen Weiss:
| N | T (ms) | T/N | T/N2 | T/(NlogN) |
|---|---|---|---|---|
| 10 000 | 100 | 0.01000000 | 0.00000100 | 0.00075257 |
| 20 000 | 200 | 0.01000000 | 0.00000050 | 0.00069990 |
| 40 000 | 440 | 0.01100000 | 0.00000027 | 0.00071953 |
| 80 000 | 930 | 0.01162500 | 0.00000015 | 0.00071373 |
| 160 000 | 1960 | 0.01225000 | 0.00000008 | 0.00070860 |
| 320 000 | 4170 | 0.01303125 | 0.00000004 | 0.00071257 |
| 640 000 | 8770 | 0.01370313 | 0.00000002 | 0.00071046 |
Hvordan måle kjøretid til et program?
Kan bruke for eksempel den statiske metoden currentTimeMillis() i klassen System, slik det er skissert nedenfor:
OBS: Ofte går algoritmene fortere enn et millisekund, og da må vi kjøre algoritmen flere ganger i en løkke, og til slutt beregne gjennomsnittet.
Oppgave
Arbeidsmengde i O-notasjon?
// 1
for (int i=0; i<N; i++){
System.out.println(i);
sum+=15;
}
//2
for(int i=0; i<N; i++){
sum=sum+i;
for (int j=0; j<N; j++){
sum=sum+j;
for (int k=0; k<N; k++)
sum=sum+k;
}
}
//3
for(int i=0; i<N; i++)
sum=sum+i;
for (int j=0; j<N; j++)
sum=sum+j;
for (int k=0; k<N; k++)
sum=sum+k;
//4
for (int i=0; i<N; i++)
for (int j=0; j<3; j++)
System.out.println(N);
//5
for (int i=0; i<N; i = i+3)
System.out.println(tab[i]);
Sortering
- Sentralt emne, fordi mange metoder baserer seg på sorterte mengder, for eksempel alle varianter av binærsøk.
- Det finnes mange sorteringsalgorimer, vi skal her se på to såkalte sekvensielle algoritmer.
- Man har estimert at 25% av all CPU-tid brukes til å sortere ditt og datt.
-
Hovedingredienser i alle sorteringsalgorimer:
- Sammenlikninger
- Ombyttinger
Sammenlikninger
- Utgangspunktet for i det hele tatt å kunne sortere, er at vi kan sammenlikne to og to elementer, og finne ut om det ene er større enn, mindre enn eller likt det andre.
- For primitive datatyper som heltall og flyttall, er dette enkelt.
- For å kunne lage generelle implementasjoner av sorteringsalgoritmer som kan ta sammenliknbare objekter som input bruker man gjerne et interface (f.eks. Comparable-interfacet i Java). Hvis en klasse implementerer et slikt interface, kan man sortere en liste med objekter av denne klassen med en metode som tar en liste av Comparable-objekter som input.
- Klassen Contact nedenfor implementerer Comparable-interfacet.
package modul2; //******************************************************************** // Contact.java Author: Lewis/Chase // // Represents a phone contact. //******************************************************************** public class Contact implements Comparable<Contact> { private String firstName, lastName, phone; /****************************************************************** Sets up this contact with the specified information. ******************************************************************/ public Contact (String first, String last, String telephone) { firstName = first; lastName = last; phone = telephone; } /****************************************************************** Returns a description of this contact as a string. ******************************************************************/ public String toString () { return lastName + ", " + firstName + ":" + phone; } /****************************************************************** Uses both last and first names to determine lexical ordering. ******************************************************************/ public int compareTo (Contact other) { int result; if (lastName.equals(other.lastName)) result = firstName.compareTo(other.firstName); else result = lastName.compareTo(other.lastName); return result; } }
Ombyttinger
I tillegg til sammenlikninger, er ombytting av to elementer en sentral ingrediens i alle sorteringsalgoritmer. Her er en slik byttemetode for en heltallstabell:
void bytt(int[] tabell, int i, int j)
{
int tmp = tabell[i];
tabell[i] = tabell[j];
tabell[j] = tmp;
}
En sorteringsalgoritme: Innsettingssortering
- Opererer med en sortert liste og en usortert liste.
- Overfører ett og ett element fra den usorterte listen til den sorterte listen.
- For hver element vi henter fra den usortere listen finner vi den korrekte plasseringen i den sorterte listen.
Algoritme for innsettingssortering
- For hvert gjennomløp
- Ta vare på neste element som skal settes inn i sortert deltabell (elementet rett etter den sorterte deltabellen).
- Forskyv alle verdier i sortert deltabell som er større enn neste ett hakk bakover i tabellen.
- Sett neste inn på den ledige plassen som da oppstår.
Det finnes mange sorteringsdemoer på nett, se f.eks.
Implementasjon for tabell med heltall
public static int [] innsettingsSort(int [] data){
// Initielt utgj��r f��rste element i tabellen som skal sorteres den
// sorterte deltabellen, resten den usorterte.
for (int i=1; i < data.length; i++){
// Tar vare p�� neste element som skal settes inn i sortert deltabell,
// og p�� nestes posisjon.
int neste = data[i];
int pos = i;
// Forskyver alle verdier i sortert deltabell som er st��rre enn neste ett hakk bakover i tabellen.
while (pos > 0 && data[pos-1] > neste){
data[pos] = data[pos-1];
pos--;
}
// Setter neste inn p�� den ledige plassen som da oppst��r.
data[pos] = neste;
}
return data;
}
Analyse av sorteringsmetoder
- Hvor mange sammenlikninger gjør vi?
- Er antallet avhengig av fordeling på input
- Finnes det et "beste" tilfelle?
- Finnes det et "verste" tilfelle?
- Kan vi si noe om det gjennomsnittlige tilfellet?
Utvalgssortering
- Virker på samme måte som innsettingssortering, men "motsatt"
- Opererer med en sortert liste og en usortert liste.
- Plukker ett og ett element fra den usorterte listen (det minste), og legger dette til sist i den sorterte listen.
- Resultatet blir en sortert liste, med det minste elementet først.
- Kan modifisere denne metoden til kun å bruke en liste (array).
Algoritme for utvalgssortering
Opererer med sortert og usortert del av tabellen som sorteres. Initielt er usortert del hele tabellen.
- For hvert gjennomløp:
- Finn minste verdi i den usorterte delen av tabellen
- La minste og første element i usortert del av tabellen bytte plass.
Bøttesortering
- Innsettingssortering og utvalgssortering er to eksempler på såkalte sekvensielle sorteringsalgoritmer. Boblesortering hører også til i denne kategorien. Disse algoritmene baserer seg på to nøstede løkker, gjør i størrelsesorden N2 sammenlikninger for å sortere N elementer og har alle arbeidsmengde som er O(N2)
- Senere i kurset skal vi se eksempler på logaritmiske sorteringsmetoder. Disse har arbeidsmengde O(NlogN), som er en nedre grense for generelle sorteringsmetoder basert på parvise sammenlikninger.
- Det finnes imidlertid sorteringsalgoritmer med arbeidsmengde som er O(N). Disse forutsetter tilleggsinformasjon om dataene som skal sorteres. Bøttesortering (bucket-sort) er et eksempel på en slik algorime, se innføring skrevet av Jan Høiberg .
Logaritmer
- For mange algoritmer, vil funksjonen for arbeidsmengde involvere logaritmen til N. Det er derfor viktig med forståelse av hva logaritmen til et tall er for noe, og hva slags algoritmer som får en kjøretid som er en funksjon av logaritmen til N.
- Logaritmer har en base (grunntall) B, for eksempel B=2 eller B=10. Vi bruker stort sett B=2.
Eksempler
Med base B =2 har vi for eksempel at
| 21 = 2, d.v.s.log22 = 1 |
| 22 = 4, d.v.s.log24 = 2 |
| 23 = 8, d.v.s.log28 = 3 |
Eksempel 1 - Gjentatt dobling
- La oss si at vi setter 1 krone i banken i år, og at beløpet dobles hvert år. Hvor mange kroner har vi da etter 5 år?
- Vi tegner tabell som viser hvordan beløpet endrer seg:
År Beløp 0 1 kr = 20 kr 1 2 kr = 21 kr 2 4 kr = 22 kr 3 8 kr = 23 kr 4 16 kr = 24 kr 5 32 kr = 25 kr - Vi ser at for hvert år kan beløpet som står i banken skrives som en potens av 2. Tallet som 2 må opphøyes i for å få beløpet i banken økes med 1 for hvert år. Logaritmen til beløpet økes med 1 for hvert år som går.
- Hvor mange år vil det ta før vi har 1024 kroner i banken?
- Hvor mange år vil det ta før vi har N kroner i banken?
Eksempel 2 - Gjentatt halvvering
- Motsatt problemstilling. La oss si at vi har 32 kroner i banken, og at beløpet halvveres hvert år. Hvor mange år går det før vi har bare 1 krone igjen?
- Tabell:
År Beløp 0 32 kr = 25 kr 1 16 kr = 24 kr 2 8 kr = 23 kr 3 4 kr = 22 kr 4 2 kr = 21 kr 5 1 kr = 20 kr - Vi ser at logaritmen til beløpet avtar med 1 for hvert år.
- Hvis vi i utgangspunktet har N kroner i banken, hvor mange år vil det da ta før vi har bare 1 krone igjen?
Søk
Problemstilling:
- Vi skal finne posisjonen til et bestemt heltall X i en tabell A med N heltall. Rekkefølgen på elementene i tabellen A skal ikke endres. Hvis X ikke finnes, skal en indikasjon på dette returneres. Hvis flere forekomster av X finnes, kan posisjonen til hvilken som helst av forekomstene returneres.
- Arbeidsmengden til en algoritme som skal løse dette problemet, avhenger av om tabellen det skal søkes i er sortert eller ikke.
Lineærsøk
Hvis tabellen vi skal søke i ikke er sortert, har vi ingen annen mulighet enn å starte på begynnelsen av tabellen og se på ett og ett element helt til vi eventuelt finner en forekomst av verdien vi søker etter. Dette kalles sekvensielt - eller lineært - søk.
Input:
- Tabellen det skal søkes i, A
- Verdien vi skal søke etter, X
Output:
- Posisjonen til en forekomst av verdien X , pos
- -1 hvis det ikke finnes noen forekomster av verdien X
Algoritme
Implementasjon
public static int linsok(int [] data, int x) {
int pos;
for (pos=0; pos < data.length ; pos++)
if(data[pos] == x)
return pos;
return -1;
}
Arbeidsmengde, Lineærsøk
N er antall elementer i tabellen. Vi skiller mellom 2 tilfeller:
- Verdien x finnes ikke i tabellen.
Arbeidsmengde O(N), siden vi da må se på alle elementene i tabellen. - Verdien x finnes i tabellen.
- Verste tilfelle:
x sise element, gir arbeidsmengde O(N). - Gjennomsnittlig situasjon:
Verdien x kan i utgangspunktet befinne seg hvor som helst i tabellen. I gjennomsnitt har vi derfor N/2 iterasjoner. Men N/2 gir også arbeidsmengde O(N).
- Verste tilfelle:
Binærsøk
Hvis tabellen det skal søkes i er sorter, kan vi bruke binærsøk. Istedenfor å starte søket fra begynnelsen av tabellen, starter vi fra midten. For hver iterasjon halveres søkeintervallet, helt til vi evetuelt finner verdien vi søker etter.
Input:
- Tabellen det skal søkes i, A
- Verdien vi skal søke etter, X
Output:
- Posisjonen til en forekomst av verdien X , mid
- -1 hvis det ikke finnes noen forekomster av verdien X
Lokale variabler:
- Posisjonsvariable for nedre og øverste element i det intervallet av tabellen vi til enhver tid søker i, nedre og ovre.
Algoritme
Implementasjon
public static int binsok(int [] data, int x) {
int nedre =0;
int ovre = data.length -1;
int mid;
while (nedre <= ovre) {
mid=(nedre+ovre)/2;
if (data[mid] < x)
nedre = mid+1;
else if (data[mid] > x)
ovre = mid-1;
else
return mid;
}
return -1;
}
Arbeidsmengde, Binærsøk
N er antall elementer i tabellen. Vi skiller mellom 2 tilfeller:
- Verdien x finnes ikke i tabellen.
Antall iterasjoner: log(N) + 1. Arbeidsmengde O(logN). - Verdien x finnes i tabellen.
- Verste tilfelle:
log(N) iterasjoner. Arbeidsmengde O(log(N)) - Gjennomsnittlig situasjon:
log(N) -1 iterasjoner. ArbeidsmengdeO(logN).
- Verste tilfelle:
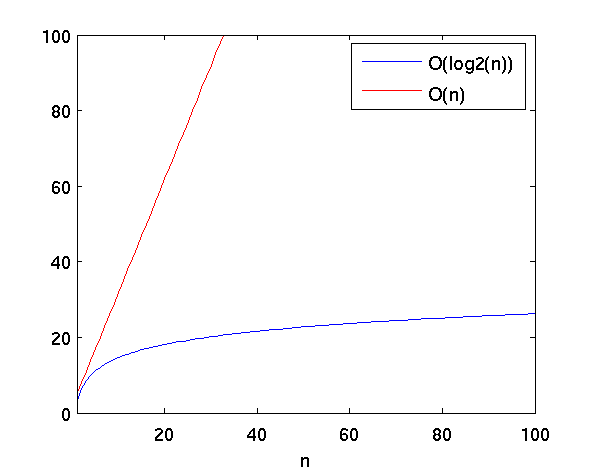
O(N) vs O(log(N))