Bezier-kurven
I modulen Polynomerhar vi løst det generelle problemet å beregne et tredjegradspolynom basert på geometriske føringer. Hermit-kurven er løsningen som er basert på at vi kjenner kurvens endepunkter og den deriverte i endepunktene. Vi har også funnet en generell form å uttrykke en slik kurve: T·MH·G.
Modulen Taylors formelbeskriver hvordan vi kan beskrive en kurve dersom vi kjenner et punkt på kurven og mange deriverte i samme punkt.
3.grads kurve
Vi tar utgangspunkt i en situasjon som er ganske like den vi hadde når vi
utviklet Hermit-kurven i modulen Polynomer.
Vi ønsker å finne koeffisientene i et tredjegradsuttrykk:
B(t)=at3+bt2+ct+d
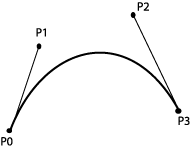
Vi vil ha geometriske føringer som er slik at kurven skal starte og slutte i to bestemte punkter, P0 og P3. Altså: B(0)=P1 og B(1)=P3. Vi skal ha et tredjegradspolynom og trenger to føringer til. Vi knytter disse til to punkter som indirekte angir den deriverte i endepunktene:
|
Vi bestemmer oss for at B'(0)=3(P1-P0) B'(1)=3(P3-P2) |
Den deriverte kjenner vi som: B'(t)=3at2+2bt+c
Det vi må gjøre er å finne a,b,c og d i dette likningssystemet:
B(0)=d=P0
B(1)=a+b+c+d=P3
B'(0)=c=3(P1-P0)
B'(1)=3a+2b+c=3(P3-P2)
Vi løser og finner:
a=-P0+3P1-3P2+P3
b=3P0-6P1+3P2
c=3P1-3P0
d=P0
og vi kan sette opp uttrykket for B(t):
B(t)=-P0t3+3P1t3-3P2t3+P3t3+3P0t2-6P1t2+3P2t2+3P1t-3P0t+P0
Vi ordner og får:
B(t)=P0(-t3+3t2-3t+1)+
P1(3t3-6t2+3t)+
P2(-3t3+3t2)+
P3(t3)
Vi har da fått en form som likner den vi hadde for Hermit-kurven og vi sette opp uttrykket i matriseform:
B(t) =T·MB·GB
der
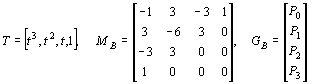
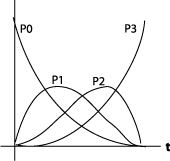
Blandingsfunksjonene er beskrevet slik:
P0: -t3+3t2-3t+1
|
|
Du kan eksperimentere med en Bezier-kurven nedenfor
La oss til slutt konstatere at vi kan skrive om:
B(t)=P0(-t3+3t2-3t+1)+
P1(3t3-6t2+3t)+
P2(-3t3+3t2)+
P3(t3)
til
B(t)=(1-t)3P0+ 3t(1-t)2P1 + 3t2(1-t)P2 + t3P3
som er den formen Bezier-kurven vanligvis framstilles på. Mer om dette nedenfor.
de Casteljau
Vi kan komme fram til Bezier-kurven på en helt annen måte, via de Casteljau-algoritmen.
Utgangspunktet er den parametriske formen på en linje som skal være slik at P(0)=P0 og P(1)=P1: P(t)=(1-t)P0+tP1. Et resonnement etter de Casteljaus algoritme fører til at dette kan oppfattes som et spesialtilfelle av en Bezier-kurve, en lineær Bezier-kurve.
Algoritmen kan beskrives etter følgende skjema, der vi hele tiden tenker oss at t løper fra 0 til 1:
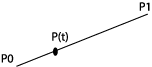
|
P(t)=(1-t)P0+tP1 |
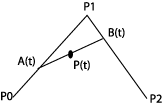
|
P(t)=(1-t)A(t)+tB(t) og: A(t)=(1-t)P0+tP1 B(t)=(1-t)P1+tP2Vi setter inn og får: P(t)=(1-t)2P0+2t(1-t)P1+t2P2 |
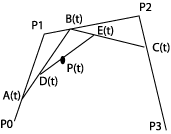
|
P(t)=(1-t)D(t)+tE(t)
og: D(t)=(1-t)A(t)+tB(t)og: A(t)=(1-t)P0+tP1Vi setter inn i to omganger og får:
P(t)=(1-t)3P0+3t(1-t)2P1+3t2(1-t)P2+t3P3
|
Det siste uttrykket er det samme som det vi kom fram til ovenfor, når vi tok utgangspunkt i et generelt tredjegradspolynom og føringer på endepunktene og den deriverte i endepunktene.
Det er lett å overbevise seg om at vi kan gjenta de Castelajau-algoritmen med ytterligere styrepunkter, P4, P5 etc.
Du kan animere de Castelau-algoritmen for 4 styrepunkter i appleten nedenfor. Flytt punktene og start animasjonen.
( En stuntapplet av Håvard Rast Blok, kl 1200 - 15.2.2001 )
Oppsummert
Uttrykket for Bezier-kurven er generelt :
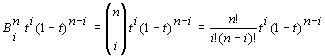
der n angir antall styrepunkter.
Kurvebeskrivelsen blir:
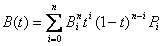
Koeffisientene,![]() ,
er de samme som de vi finner i Pascals trekant:
,
er de samme som de vi finner i Pascals trekant:
| 1 | ||||||||
| 1 | 1 | |||||||
| 1 | 2 | 1 | ||||||
| 1 | 3 | 3 | 1 | |||||
| 1 | 4 | 6 | 4 | 1 |
Vi har benyttet n=4, og brukt koeffisientene 1, 3, 3, 1.
Kurvesegmenter
Den generelle formen på Bezier-kurven gir oss mulighet for å spesifisere flere styrepunkter. Vi kan f.eks. la n=5 og får:
B(t)=(1-t)4P1 + 4t(1-t)3P2 + 6t2(1-t)2P3 + 4t3(1-t)P4 + t4P5
Vi skal ikke utvikle dette resonnementet for å handtere lengre kurver. Vi vil heller betrakte en kurve som sammensatt av flere kurvesegmenter.
Vi vil kikke litt på hvordan vi kan skjøte kurver og oppnå ulik grad av glatthet. Vi vil konsentrere oss om hvilke betingelser som må være tilstede dersom to segmenter skal henge sammen på en "glatt" måte. Vi ser på fire grader av geometrisk kontinuitet. Vi betrakter Bezierkurver og framstiller dem slik vi oftest finner dem i tegneprogrammer. Linjene mellom styrepunktene framstilles som "handtak" som vi kan ta tak i for å endre kurveformen.
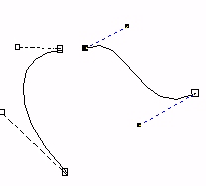 |
Ingen kontinuitet. De to kurvesegmentene har ikke noe felles punkt. |
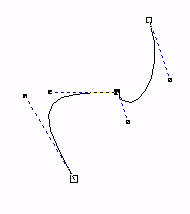 |
De to kurvesegmentene har et felles punkt. Kurvene henger sammen men har en tydelig knekk. De deriverte (for høyre segment og venstre segment) i dette punktet er forskjellige både i retning og størrelse. |
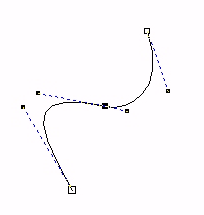 |
De to kurvesegmentene har et felles punkt, og skjøten er ganske glatt. De deriverte i dette punktet har samme retning. |
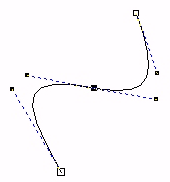 |
De to kurvesegmentene har et felles punkt, og skjøten er glatt. De deriverte i dette punktet har samme retning og samme størrelse. |
Beregning
Selv om OpenGL har mekanismer for å tegne Bezier-kurver, er det ofte vi ønsker å "handtegne" Bezier-kurver. Kanskje vi vil benytte kurven i et vanlig vindu, uten OpenGL. Ofte i forbindelse med en interaktiv manipulasjon av styrepunktene. Da er det greitt å finne en effektiv beregningsmåte for et tilstrekkelig antall punkter på kurven til at vi får en form som er tilstrekkelig glatt å se på.
Hvis vi bestemmer oss for at vi holder oppløsningen fast, si at vi vil beregne kurven for m t-verdier inklusive 0 og 1. Vi ser av uttrykket for kurven at vi kan beregne og tabulere m verdier av (1-t)3, (1-t)2, (1-t), t3, t2, t. Ialt en 6 x m tabell. Dersom styrepunktene flytter seg, kan vi beregne den nye kurven ved hjelp av tabellen. Antall multiplikasjoner reduseres kraftig med en slik strategi.
Vi kan i tillegg nøye oss med å beregne nye verdier i det t-området der den nye kurven er signifikant, synlig, forskjellige fra den forrige. Riktignok ser vi av Bezier-kurvens vektfunksjoner at alle styrepunkter påvirker et helt kurvesegment, men forskjellen kan være mindre enn det som er synlig på skjermen. Dette fordrer selvsagt at vi tar vare på den gamle kurven for å kunne sammenligne. Dersom vi har kurver av høyere orden enn 3, eller har skjøtet kurvesegmenter, aktualiseres denne strategien.
Flater
Vi kan generalisere Bezier-kurver til Bezier-flater.
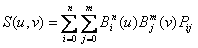
Vi ser da for oss styrepunkter som ligger i et nett, og vi kan beregne kurver langs begge retningene i nettet og interpolere. OpenGL håndterer dette. Modulen Påskeegg bruker en Bezier-flate. Det samme gjøres i modulen Trampoline.
I OpenGL
Rene Bezierkurver handteres direkte av OpenGL
// 4 controlpoints in space
GLfloat ctrlpoints[4][3] = {
{-4.0,-4.0,0.0},
{-2.0,4.0,0.0},
{2.0,-4.0,0.0},
{4.0,4.0,0.0} };
// we want to draw with t from 0.0 to 1.0
// and we give the dimensions of the data
glMap1f(GL_MAP1_VERTEX_3,0.0,1.0,3,4,& ctrlpoints[0][0]);
glEnable(GL_MAP1_VERTEX_3);
// draw a curve with 30 steps from t=0.0 to t=1.0
glBegin(GL_LINE_STRIP);
for (int i=0;i<=30;i++)
glEvalCoord1f((GLfloat) i/30.0);
glEnd();
Flater, fra modulen Trampoline
// define ctrlpoints for trampoline
GLfloat ctrlpoints[4][4][3] = // [v][u][xyz]
{
{ {-1.5f,-1.5f,0.0f}, {-0.5f,-1.5f,0.0f},
{0.5f,-1.5f,0.0f}, { 1.5f,-1.5f,0.0f}
},
{ {-1.5f,-0.5f,0.0f}, {-0.5f,-0.5f,0.0f},
{0.5f,-0.5f,0.0f}, {1.5f,-0.5f,0.0f}
},
{{-1.5f,0.5f,0.0f}, {-0.5f,0.5f,0.0f},
{0.5f,0.5f,0.0f}, {1.5f,0.5f,0.0f}
},
{ {-1.5f,1.5f,0.0f}, {-0.5f,1.5f,0.0f},
{0.5f,1.5f,0.0f}, {1.5f,1.5f,0.0f}
}
};
...
// uttegning
glMap2f(GL_MAP2_VERTEX_3,0.0f,1.0f,3,4,0.0f,1.0f,12,4,
& ctrlpoints[0][0][0]);
glEnable(GL_MAP2_VERTEX_3);
glMapGrid2f(20,0.0f,1.0f,20,0.0f, 1.0f);
glEvalMesh2(GL_FILL, 0, 20, 0, 20);


